Today, OpenSSL 1.0.2d has been released. Many lines of code have been changed, but most important is a Security Fix that allowed an attacker to bypass certain checks on certificates. The problem is summarized in the changelog of the new release:

Changes between 1.0.2c and 1.0.2d [9 Jul 2015]

*) Alternate chains certificate forgery

During certificate verfification, OpenSSL will attempt to find an alternative certificate chain if the first attempt to build such a chain fails. An error in the implementation of this logic can mean that an attacker could cause certain checks on untrusted certificates to be bypassed, such as the CA flag, enabling them to use a valid leaf certificate to act as a CA and “issue” an invalid certificate.

This issue was reported to OpenSSL by Adam Langley/David Benjamin (Google/BoringSSL).
[Matt Caswell]

How does certificate validation work?

In general, when validating an X.509 certificate (for example when accessing a website using https), the validator has a list of trusted authorities (effectively the list of CAs in your browser), the certificate to validate and possibly also a list of helper certificates that can be used to establish a chain of trust to one of the trusted authorities. Certificate validation is a two step process. At first, a path from the certificate to a trusted authority is established, then this path is verified. There might be more than one path, and should verification fail, another path might be determined and verification is tried again.

How does the attack work?

Fortunately, included in the patch is also an additional test for OpenSSL in crypto/x509/verify_extra_test.c that describes the problem in detail. The scenario outlined here is the following:

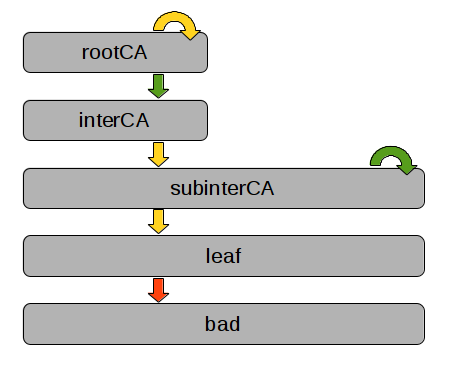
Arrows are certificates, grey boxes denote entities. The two certificates in green are trusted by the verifier. Both subinterCA certificates (the self signed one and the one signed by interCA) share of course the private key. The attacker is in possession of the leaf certificate with the corresponding private key, which is a normal client certificate without CA=true. This scenario might be common for CAs that start independently, and are later on signed by another CA.

When the attacker uses the private key of the leaf certificate to sign another certificate for bad, it should be rejected since the leaf certificate does not have CA=true set. However, OpenSSL fails to reject this certificate properly when the interCA->subinterCA and the subinterCA->leaf certificates are provided as (untrusted) auxiliary certificates.

Who is affected?

Probably anyone who uses client certificate authentication for his webserver. However this is still very uncommon, since username/password authentication is still the most common form of authentication on the web.

Countermeasures

The best countermeasure here is to update OpenSSL to 1.0.2d or a later version. Alternatively (NOT RECOMMENDED) it might be possible to accept only certificates that are known by the server with tools such as stunnel and setting verify=3. Also, such scenarios with multiple paths for a single certificate might be avoided.

Today, Maxime Augier gave a great talk about the state of security of the internet PKI infrastructure. The corresponding paper written by Lenstra, Hughes, Augier, Bos, Kleinjung, and Wachter was uploaded to eprint.iacr.org archive a few weeks ago. In a nutshell, they found out that some RSA keys, that is often used in the SSL/TLS protocol to secure internet traffic, are generated by bad pseudo random number generators and can be easily recovered, thous providing no security at all.

The RSA cryptosystem

RSA is one of the oldest and most famous asymmetric encrytion schmes. The key generation for RSA can be summarized as follows:

For a given bitlength l (for example $latex l = 1024$ or $latex l = 2048$ bits), choose randomly two prime numbers p and q of of bitlength $latex l/2$. Choose a number $latex 1 < e < (p-1)*(q-1)$, that has no divisor in common with $latex (p-1)*(q-1)$. Many people choose $latex e = 2^{16+1}$ here for performance reasons, but other choices are valid as well. Now, the number $latex n = p*q$ and e form the public key, while $latex d = e^{-1} \bmod (p-1)*(q-1)$ is the private key. Sometimes, the numbers p and q are stored with the private key, because they can be used to accelerated decryption.

To encrypt a message m, one just computes $latex c = m^e \bmod n$, and to decrypt a message, one computes $latex m = c^d \bmod n$. However, we don’t need that for the rest of this text can safely ignore that.

How random do these numbers need to be?

When generating cartographic keys, we need to distinguish between just random numbers and cryptographically secure random numbers. Many computers cannot generate real random numbers, so they generate random numbers in software. For many applications like computer games and for example simmulations of experiments, we only need number that seem to be random. Functions like “rand()” from the standard c library provide such numbers and the generation of these numbers is often initialized from the current system time only.

For cryptographic applications, we need cryptographically secure random numbers. These are numbers that a generated in a way, that there is no efficient algorithm, that distinguish them from real random numbers. Generating such random numbers on a computer can be very hard. In fact, there have been a lot of breaches of devices and programs, that used a bad random number generator for cryptographic applications.

What has been found out?

From my point of view, the paper contains two noteably results:

Many keys are shared by several certificates

6 185 228 X.509 certificates have been collected by the researchers. About 4.3% of them contained an RSA public key, that was also used in another certificate. There could be several reasons for this:

• After a certificate has expired, another certificate is issued, that contains the same public key. From my point of view, there is nothing wrong with doing that.
• A company changes their name or is taken over by another company. To reflect that change, a new certificate is issued, that contains another company name, but still uses the same key. I don’t see any problems here either.
• A product comes with a pre-installed key, and the consumer has to request an certificate for that key. The same key is shipped to several customers. From my point of view, this is really a bad idea
• Or there might be really a bad random number generator in some key generation routines, that two entities that are not related come up with the same RSA public (and private) key. This is a security nightmare.

Some keys share a common divisor

This is definitely not supposed to happen. If two RSA keys are generated, that share a common divisor by the same or by different key generation routines, the private key for both public keys can be easily determined, and the key generation routine is deeply flawed.

What are the consequences?

For those, who use an RSA public key, that shares a modulus with another different RSA public key, their key provides no protection at all. All implementations, that generated these keys definitely need to be updated and the certificates using the weak keys need to be revoked.

Which devices and vendors are affected?

Because disclosing the list of affected devices and vendors would compromise the security of these systems immediately, and allow everyone to recover their secret RSA keys, this has not been disclosed.

A reference implementation of the GMR-1 cipher has now been released. You can download the sourcecode from http://cgit.osmocom.org/cgit/osmo-gmr/tree/src/l1/a5.c.

Here are the most important facts in a nutshell:

• 4 Linear Feedback Shift registers in Fibonacci configuration.
• 81 bits of state
• Registers 1, 2, and 3 of length 19, 22, and 23 bits control the output
• Register 4 of length 17 bits controls the clocking of registers 1, 2, and 3, and does not contribute to the output
• Clocking control is a simple majority clocking, so that registers are clocked 0 or 1 times
• The output combiner is a quadratic function

So in fact, this cipher looks like a A5/2 clone from GSM.